统计过程控制 SPC 控制图的设计原理

统计过程控制主要是对生产过程和生产状态进行分析，通过适当的措施达到和保持过程的稳定性，从而达到提高和保证产品质量的目的。控制图是统计过程控制中最有效的工具之一，也是统计过程控制的技术基础。控制图是指利用概率统计原理，在普通坐标纸上制作两条控制线和一条中心线，然后将按时间顺序采样得到的特征值以散点图的形式依次绘制在坐标图上，从点的动态分布来讨论过程质量及其趋势的图。

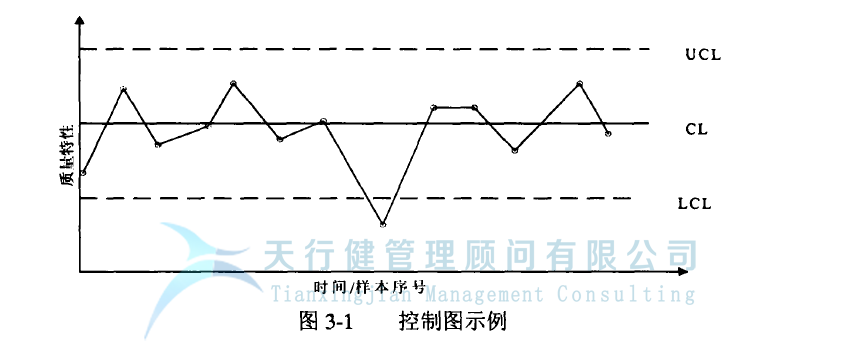
控制图的基本格式如图3-1所示。横坐标是按时间顺序排列的样品序号，纵坐标是产品质量特征值或样品统计量。通常使用中心线，表示为CL(控制极限)，两个控制极限通常用虚线表示。中心线以上的控制界限线为上控制线，表示为UCL(控制上限)；中心线以下的控制限线为下控制线，称为LCL(控制下限)。

控制图的设计原则可以概括为四句话，即正态性假设、3σ准则、小概率原则和反证法思想。

(1)正态性假设

在任何生产过程中，被监控的质量特征值总会有一定程度的波动。当过程稳定或过程受控时，这些波动主要来自SM1E(人-机-料-法-测-环境)微小变化引起的随机误差。天行健咨询一家专注于精益生产管理的管理咨询公司，六西格玛管理培训和项目咨询。此时，根据大数定律，大多数质量特征值服从或近似服从正态分布。这个假设叫做正态假设。基于这一假设，我们可以利用正态分布的一些固有特性来建立过程控制模型。

(2) 3σ准则

如果质量特征数据服从正态分布，我们知道距离配送中心μ3σ(即3σ)范围内的面积为99.73%。如果生产过程仅受随机原因影响，则该过程的产品质量特征数据应以99.73%的概率落在此范围内，即:

P{μ-3σ<X<μ+3σ}=99.73%

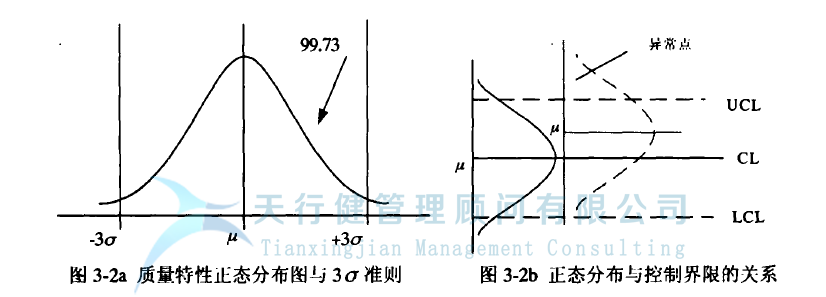
如果有更多的数据落在这个范围之外，则判断生产过程中有异常(图3-2a和图3-2b)。例如，以一个角度将图3-2a变成图3-2b的形状，即控制图的基本形状。其中：UCL=μ+3，LC=μ， LCL=μ-3σ。

(3)小概率原理

小概率原理，即认为小概率事件一般不会发生。根据3σ法则，当X服从正态分布N (μ-σ 2)时，X落在控制限外的概率仅为0.27%。即:1-P{μ-3σ<x<μ+3σ}=0.27%

因此，我们有理由认为，在正常情况下，X不应该超过控制极限。小概率原理服从人的推理思维，所以也叫实用推理原理。当然，小概率原理的应用也可能导致错误，但造成错误的可能性恰恰是这种小概率事件发生的概率。天行健咨询一家专注于精益生产管理的管理咨询公司，六西格玛管理培训和项目咨询。

(4)反证法思想。

一旦控制图上的想法出界或其他小概率事件发生，就有理由怀疑原来的生产过程失控，即生产过程不稳定。这时候就要及时找出原因，确认生产过程是否发生了重大变化，进一步分析是什么原因导致了这种变化。